BANCO DE INFORMACIÓN - MECÁNICA INDUSTRIAL - ITESARC
Recurso disponible para que los estudiantes puedan acceder a los documentos relacionados con el proceso formativo virtual, de la especialidad de mecánica industrial del ITESARC.
Los engranajes rectos tienen los dientes montados en ejes paralelos, lo que hace que sean de gran utilidad cuando lo que se desea es trasladar movimiento desde un eje hacia otro que se encuentre próximo y también paralelo.
Además de muy fiables, los engranajes rectos destacan porque en ellos no se produce un empuje axial, precisamente por el hecho de que tengan los dientes paralelos a su eje.
Partes de un engranaje recto
Las diferentes partes que podemos diferenciar en un engranaje recto son las siguientes:
Dientes. Los dientes del engranaje son los que se encargan de llevar a cabo el esfuerzo de empuje, por lo tanto son los elementos que transmiten la potencia desde el eje conductor al conducido. Durante su fabricación y diseño se tiene en cuenta un perfil característico definido.
Circunferencias. Podemos distinguir entre la primitiva (Rp), a lo largo de cuya extensión se engranan todos los dientes; la interior (Ri), que es la que pasa por la base de los pies de los dientes y donde se limita el pie del diente; y la circunferencia exterior (Re), que es la que limita la parte exterior del engranaje. El pie de diente es la parte de este que se encuentra entre la circunferencia primitiva y la circunferencia interior.
Analizando de manera diametral tenemos que:
Donde:
Z, Número de dientes
Dp, Diámetro primitivo
De, Diámetro exterior
Di, Diámetro interior
P, Paso circular
M, Módulo
H, Altura total del diente
CALCULO DE PIÑON RECTO
En primer lugar, es necesario definir una serie de conceptos para efectuar el cálculo de engranajes rectos:
Número de dientes (z). Su valor es: z = d/m
Módulo (m). Relación entre la medida del diámetro primitivo expresado en milímetros y el número de dientes. En los países anglosajones se emplea otra el “Diametral Pitch”, que es inversamente proporcional al módulo. El valor del módulo se fija mediante cálculo de resistencia de materiales en virtud de la potencia a transmitir y en función de la relación de transmisión que se establezca. Dos engranajes que engranen tienen que tener el mismo módulo.: m = d/z
Diámetro Primitivo (Dp), Es el diámetro correspondiente a la circunferencia primitiva su valor es: Dp = m x z
Diámetro Exterior (De). Es el diámetro correspondiente a la circunferencia exterior su valor es: De = m (z + 2); De = Dp + 2m
Diámetro Interior (Di). Es el diámetro correspondiente a la circunferencia interior, su valor es: Di = m (z – 2,5) ó Di = De – 2h
Distancia entre Centros (dc). Es la distancia entre los ejes de la rueda y el piñón, su valor es: dc = (D + d) / 2, conde “D” corresponde al diámetro primitivo del engranaje y “d” al diámetro primitivo del piñón.
En los módulos normalizados, deberán ir clasificados; los módulos de 1 a 4 varían de 0,25 en 0,25; los módulos de 4 a 7 varían de 0,5 en 0,5, los módulos de 7 a 12 varían de 1 en 1; y, por último, los módulos de 12 a 20 varían de 2 en 2.
Si tenemos la pulgada en lugar de los centímetros como unidad de longitud, para establecer el cálculo de engranajes rectos necesitaremos definir el llamado ‘diámetro Pitch’, que es el equivalente al número de dientes por pulgada que se localizan en el diámetro primitivo. La relación que hay el diámetro Pitch y el módulo es de m= 25,4/Pt.
Veamos un ejemplo de aplicación:
Para llevar a cabo el cálculo se inventa un módulo M entre 1.75 y 4.0, los cuales se incrementan de 0.25 en 0.25. Es decir: 1.75, 2.0, 2.25, 2.50, 2.75, 3.0, 3.25, 3.50, 3.75, 4.0. Los del ITESARC !
Tomamos por ejemplo M=2.0 con un De= 74.0 mm. (De < 76.2 mm).
Aplicando fórmulas, tenemos que:
De = Dp + (2xM) , reemplazamos los valores....
74.0 mm = Dp + (2x2.0)
74 = Dp + 4
74 - 4 = Dp
70 mm = Dp
Cómo Z= Dp / M = 70.0 / 2.0 = 35
H= 2.167 x M = 2.167 x 2.0 = 4.3 mm
PROCEDIMIENTO PARA EL TALLADO DE PIÑON RECTO
Observemos atentamente el paso a paso:
NORMAS TECNICAS A TENER PRESENTE
El principal referente normativo es la NTC 1140. Esta norma se aplica a los engranajes de mecánica general, fresados, tallados y
rectificados, cilíndricos de dentado recto, helicoidal o doble helicoidal, exteriores e interiores
con perfil del diente en evolvente de círculo y ángulo de presión de 20º.
La Asociación Americana de Fabricantes de Engranajes AGMA es una organización estadounidense que desarrolla normas orientadas hacia la manufactura de engranajes. Junto con el
Instituto Nacional de Estándares Americanos ANSI han publicado la norma ANSI/AGMA
2001-D04 llamada ”Factores fundamentales y métodos de cálculo para la capacidad de carga
de engranajes con dientes helicoidales y rectos con perfil de evolvente”. Esta norma consta de
una sola parte y fue publicada en el año 2004 como nueva versión de su predecesora AGMA
2001-C95 de 1995.
La Organización Internacional de Normalización ISO desarrolla y publica norma internacionales en diferentes ámbitos, siendo el ramo industrial uno de sus focos. La ISO 6336 es
titulada ”Cálculo de la capacidad de carga de engranajes de diente recto y helicoidal”, y está compuesta por once apartados, unos establecidos como normas, otros como especificaciones
técnicas, y otros como reportes técnicos.
Estudiante, revise detenidamente cada una de las actividades relacionadas (Lista de Actividades).
El desarrollo de cada actividad se debe realizar con su puño y letra, tomando registro fotográfico del resultado para enviarlo como evidencia en la fecha establecida mediante el correo electrónico.
Ante cualquier inquietud y/o dificultad debe contactar oportunamente al docente para la respectiva orientación académica. Vía correo electrónico, Mensaje Whatsapp, o durante los encuentros virtuales en Google Meet.
Las actividades son de responsabilidad individual (mientras que el docente no indique otra metodología) y se recalca la importancia de la honestidad y compromiso que amerita este proceso de formación virtual por parte de todos los estudiantes.
CONDICIONES DE ENTREGA:
Enviar evidencia del desarrollo de cada actividad al correo electrónico del docente:
Las máquinas fresadoras pueden ejecutar una gran cantidad de operaciones complejas, como cortes de ranuras, planificación, perforaciones, encaminado, etcétera, siendo el cabezal universal divisor, una pieza muy importante, para que esta máquina herramienta realice estas tareas. El conocimiento de este elemento nos capacita para entender, analizar y estudiar una de las máquinas herramientas más versátiles y usadas de la industria. La fresadora en la que nos basamos era una fresadora universal, pero los principios básicos de funcionamiento son los mismos.
Veamos en detalle este importante elemento:
CABEZAL UNIVERSAL DIVISOR
El cabezal universal divisor es un accesorio de la fresadora, en realidad es uno de los accesorios más importantes, diseñado para ser usado en la mesa de la fresadora. Tiene como objetivo primordial hacer la división de la trayectoria circular del trabajo y sujetar el material que se trabaja. El eje portafresas que posee el cabezal se coloca formando cualquier ángulo con la superficie de la mesa. Este accesorio se acopla al husillo principal de la máquina, permitiéndole realizar las más variadas operaciones de fresado.
El cabezal universal es uno de los más comúnmente usados en la industria. Se usa para ejecutar todas las formas posibles de divisiones. Es un accesorio muy preciso y versátil. Sujeta la pieza en uno de sus extremos, bien sea en la copa universal, entre copa y punta o entre puntas y es posible producirle un movimiento giratorio a la pieza en combinación con el movimiento longitudinal de la mesa para el fresado de hélices.
El cabezal divisor se necesita para la fabricación de piezas en las que hay que realizar trabajos de fresado según determinadas divisiones (ruedas dentadas, cuadrados y hexágonos, árboles de chavetas múltiples, fresas, escariadores). Con su ayuda también es posible fresar ranuras en espiral.
Constitución:
Los divisores universales pueden variar en su diseño y forma, pero su principio de funcionamiento es el mismo.
Su estructura fundamental tiene dos partes:
La base es un caja de hierro fundido que se fija en la mesa de la fresadora, se fija en el bastidor. Presenta una cornisa circular que permite al cabezal girar en el plano vertical. Tiene escala graduada para fijar los grados.
Su objetivo principal es servir de cuna al cuerpo orientable.
Lleva una escala de referencia que permite controlar la inclinación del cuerpo orientable.
BASE (A)
CUERPO ORIENTABLE
Es una carcaza con dos extremos salientes cilíndricos, los cuales se apoyan en la base del divisor y permiten orientar e inclinar el eje del husillo a cualquier ángulo respecto de la mesa.
Dentro de sí contiene el conjunto de órganos, que es la parte más importante del divisor, y que permite dar a la pieza los movimientos para hacer cualquier número de divisiones.
El cuerpo suele dividirse en dos partes, una parte (B) que se adapta a la base apoyada en el bastidor, el cual tiene otra colisa circular; y la otra parte (C) del cuerpo que es la que contiene el portafresas y puede girar en un plano perpendicular al de la colisa de la base.
El cabezal divisor (aparato divisor universal) (Figura 1) consta de la carcasa en que va soportado el husillo del cabezal divisor. Este husillo sirve para alojar el montaje de sujeción. Las piezas a trabajar pueden sujetarse en voladizo o entre puntos. El disco divisor va fijado sobre el husillo del cabezal. En el aparato divisor también existe un mecanismo de tornillo sin fin necesario para la división indirecta, así como un dispositivo para la división diferencial y para el fresado de ranuras helicoidales.
Figura 1: Cabezal divisor
Funcionamiento
El movimiento de rotación llega al husillo secundario o portafresas a través del eje intermediario que se monta en el husillo principal.
A este se acopla el sistema de engranajes del mecanismo interior del aparato.
Procesos de montaje de un cabezal universal en la fresadora
1. Se monta el eje intermedio entre el cabezal universal y el husillo de la máquina.
Limpiamos el cono del eje intermedio y el cono del husillo principal.
Introducimos el eje intermediario y fíjelo con el tirante.
Atención: Hay que cuidar que las ranuras del eje penetren en las chavetas de arrastre del husillo.
2. Colocamos el Cabezal Universal
Hacemos coincidir las referencias que indican la posición correcta.
Limpiamos las superficies que estén en contacto, tanto del cabezal universal como de la máquina.
Como algunos ejes intermedios tienen en su extremo una chaveta de arrastre, estrías o un engranaje, debemos cuidar que haya una conexión correcta con los órganos internos del cabezal universal.
Se coloca una tabla o una lámina de material blando entre la superficie de la mesa y el cabezal universal
Nota: hay que ser precavido, para trasladar el cabezal universal es recomendable hacerlo con ayuda de otras personas, o se puede utilizar, también, un elevador mecánico.
3. Fijamos el Cabezal Universal
Introducimos los tornillos y apretamos con suavidad.
Al final, debemos apretar con fuerza para que los tornillos queden bien colocados.
Ventajas del Cabezal Universal Divisor
El cabezal universal divisor sirve como accesorio para el montaje de piezas; se inclina para facilitar el fresado en ángulo; permite hacer cualquier número de divisiones. Sirve también como Divisor Simple. Esto se puede lograr por tener sobre el husillo un plato divisor con ranuras que permite el operarlo directamente, si antes se ha desconectado el tornillo sinfín de la corona.
Mantenimiento
El divisor universal es muy valioso y delicado. No debe golpearse. El transporte debe ser muy cuidadoso. Hay que mantenerlo siempre limpio y lubricado.
Montaje de piezas
El montaje de piezas sobre el cabezal divisor universal permite hacer en la fresadora ciertas operaciones que de otro modo sería muy difícil o imposible de hacer.
Por ejemplo:
Lograr que la pieza gire en relación y simultáneamente con el desplazamiento de la mesa (engranajes helicoidales, brocas, sinfín).
Dividir regularmente la periferia de una pieza (anillos graduados, ruedas dentadas).
Fresar piezas en ángulo (engranaje cónico).
Clasificación:
Los montajes para mecanizar piezas en el aparato divisor, podemos agruparlos en tres:
Montaje al aire
Montaje entre puntas
Montaje entre copa y punta
Estos son montajes típicos de torno.
La misma disposición de la nariz del husillo, tanto del torno como del cabezal divisor universal, como también los mismos elementos empleados, (copas, puntos de centraje, contrapunta, bridas, …) permiten efectuar los montajes en forma similar.
En el cabezal divisor universal se puede aplicar el sistema de división directa, como si se tratara de un divisor simple.
En el procedimiento de división directa no están engranados el tornillo sin fin y la rueda helicoidal. El engrane se obtiene en virtud del giro de un cojinete rotativo excéntricamente en que va soportado el tornillo sin fin. La división se produce en un disco divisor que generalmente tiene 24 agujeros o muescas (entalladuras) pero algunas veces también 16, 36, 42 ó 60.
El disco divisor en el que encaja un punzón divisor, está fijado al husillo del cabezal. En cada paso de división, el disco divisor y con él la pieza girada en las correspondientes distancias entre agujeros. No pueden obtenerse más divisiones que las que permiten, sin resto, el número de agujeros o muescas del plato divisor. De este modo pueden realizarse divisiones son dispositivos sencillos, que generalmente poseen discos recambiables. Mediante la división directa se opera más rápidamente que con los otros procedimientos.
El divisor universal funciona en esta forma por tener un planto con ranuras, fijo al husillo principal, y un trinquete que encaja en las ranuras.
Generalmente el plato trae 24 ranuras, pero algunos traen 16 – 32 – 42 ó 60 ranuras.
La siguiente es la fórmula para la división directa con cabezal divisor universal:
F = K / N
F = número de ranuras que se deben girar
K = número de ranuras del plato
N = número de divisiones que se requieren
Observaciones
La división directa es muy limitada.
Es aplicable cuando las divisiones que se requieren obtener corresponden a un submúltiplo del número de ranuras del plato.
Para fresar cada cara es necesario encajar el trinquete en la ranura correspondiente y bloquear el husillo del cabezal.
No hay que contabilizar la ranura donde quedó el trinquete para la nueva división.
Desencajar el trinquete para cada nueva división.
Si el cabezal lo permite, aislar el husillo de la rueda (corona) ya que el movimiento entre ambos no es necesario.
División Indirecta
Es uno de los sistemas de división que permite obtener un determinado número de divisiones, que no se lograrían por la división directa.
En la división indirecta el husillo del cabezal divisor es accionado a través de un tornillo sin fin y una rueda helicoidal. La relación de transmisión del mecanismo de tornillo sin fin es 40 : 1, es decir que 40 revoluciones de la manivela divisora suponen una revolución del husillo del cabezal divisor. Si, por ejemplo, se quiere tener una división decimal, para cada paso parcial serán necesarias 40 : 10 = 4 vueltas de la manivela divisora.
Para 32 divisiones, por ejemplo, se necesitarán 40 : 32 = 1 8/32 = 1 ¼ revoluciones. Para poder realizar el ¼ de revolución, hará falta un disco de agujeros con una circunferencia de agujeros cuyo número sea divisible por 4, por ejemplo la circunferencia de 16 agujeros daría ¼ de 16 = 4. La manivela divisora desplazable radialmente se ajusta en esta circunferencia de agujeros y se hace girar en 4 distancias entre agujeros. En este procedimiento de división se sujeta el disco de agujeros mediante la clavija de fijación.
Los discos de agujeros (Figura 23) son recambiables. Tienen por lo general de seis a ocho circunferencias concéntricas de agujeros con diferentes números de agujeros. Dentro de cada circunferencia las distancias entre agujeros son iguales. La división se facilita mediante la utilización de la tijera de dividir (Figura 24). Se ahorra uno el tiempo perdido en el engorroso recuento de agujeros, expuesto además a equivocaciones. Entre ambos brazos de la tijera siempre tiene que haber un agujero más que el número de espacios entre ellos que se había calculado. Para evitar errores en la división hay que tener cuidado al seguir dividiendo, de que la manivela gire siempre por error, habrá que retroceder suficientemente la manivela para eliminar la acción del recorrido muerto, y entonces volver a girar hacia delante.
También pueden realizarse por el procedimiento indirecto divisiones que vayan dadas en forma de ángulo.
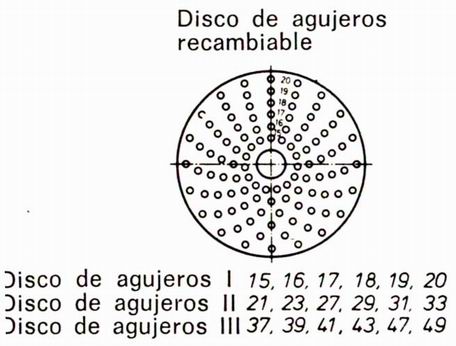
Figura 23:Discos de agujeros
Figura 24:Empleo de la tijera en la división
Las operaciones de cálculo se ejecutan tomando como base la relación existente entre el tornillo sinfín y el número de dientes de la corona.
La regla para determinar el número de vueltas de la manivela, el número de agujeros y la circunferencia de agujeros del disco divisor, así:
Consideremos la relación 1/40, o sea que la corona tiene 40 dientes y el tornillo sinfín una entrada. Cuando hayamos dado una vuelta en el tornillo sinfín, la corona habrá desplazado un diente y el husillo 1/40 de vuelta.
Si hacemos girar la manivela 20 vueltas, la corona se habrá desplazado 20 dientes, y por lo tanto, el husillo con la pieza habrá dado ½ vuelta.
Para saber el número de vueltas que se deben dar a la manivela con objeto de lograr un determinado número de divisiones en el husillo, aplique la siguiente fórmula:
F = K / N
F = número de vueltas de la manivela
K = número de dientes de la corona
N = número de divisiones por efectuar
División Angular
La división angular es otro de los sistemas de división que se pueden realizar con la ayuda del cabezal divisor universal, cuando la medida entre divisiones sobre una circunferencia está dada en grados y minutos.
El ángulo entre divisiones tiene su vértice en el centro de la pieza.
División en grados:
Como el husillo del cabezal gira 360 grados en una vuelta, en una sola vuelta de la manivela gira
360/40 = 9 grados (con una relación de 1/40)
Por tanto, si se quiere desplazar un número determinado de grados, se aplica la siguiente fórmula:
La división diferencial constituye una ampliación del procedimiento indirecto de división. Se emplea en lo casos en que no es posible la división indirecta por no existir en ninguno de los discos los agujeros, las circunferencias de agujeros necesarias. Se elige por ello un número auxiliar de división (T´) que pueda ser obtenido por división indirecta y que pueda ser mayor o menor que el número pedido (T). La diferencia resultante (T´ - T) se compensa mediante un movimiento de giro del disco de agujeros se produce partiendo del husillo del cabezal a través de ruedas de cambio. Debe marchar paralelamente al movimiento de la manivela de división cuando T´ es mayor que T, tener sentido opuesto cuando T´ se eligió menor que T. En la división diferencial el disco de agujeros no debe quedar sujeto a la carcasa mediante la clavija de fijación, tal como suceda en la división indirecta (Figura 25). Tiene que poder girar, con la clavija suelta.
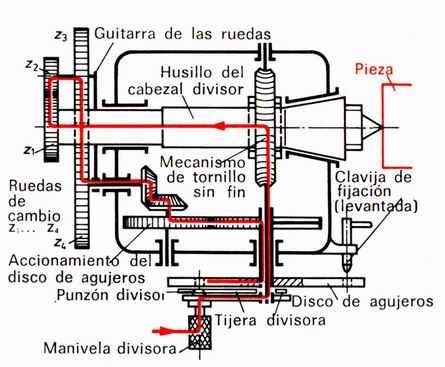
Figura 25:Divisor diferencial.
Fresado de ranuras espirales
En el fresado de ranuras (ranuras helicoidales), como por ejemplo en la fabricación de fresas con un dentado especial, de escariadores, de brocas espirales, así como de brocas helicoidales, es necesario que el útil realice durante el proceso de fresado un movimiento rectilíneo y uno de rotación.
El movimiento rectilíneo de avance se realiza por medio del husillo de mesa. El movimiento uniforme de giro se produce partiendo del husillo de mesa, a través de ruedas de cambio, ruedas cónicas, ruedas rectas, disco de agujero, clavija divisora, tornillo sin fin y rueda helicoidal, sobre el husillo del cabezal divisor (Figura 26). No pueden proveerse de ranuras espirales nada más que las piezas cuya división pueda realizarse por el método indirecto. En el fresado de ranuras helicoidales hay que elegir la relación de dientes de las ruedas de cambio de tal modo que el avance de la mesa para una revolución completa de la pieza sea igual al paso pedido para la hélice.
Figura 26:Fresado de ranuras helicoidales.
La pieza tiene que colocarse mediante basculación de la mesa de la máquina oblicua al eje de la pieza con oblicuidad igual al ángulo de posición o de ajuste b . Esto no resulta posible de conseguir nada más que en una fresadora universal o en una máquina fresadora dotada de un cabezal basculante.
Si las piezas han de llevar varias ranuras espirales, tendrá que realizarse la división de la distintas ranuras igualmente con el cabezal divisor.
Con objeto de disminuir la proporción, a veces importante, de los tiempos invertidos en la de fresar, así como para satisfacer las más altas exigencias en cuanto a precisión, se emplean aparatos divisores ópticos, hidráulicos, neumáticos y electro-automáticos.
Ejercicios de Aplicación
Conseguir 10 divisiones en una pieza. N=40
Fórmula 40 / N ; reemplazando tenemos 40 / 10 = 4
Es decir, son 4 vueltas exactas para cada división.
Caso A: Cuando N>40
Tomemos como ejemplo N=76, aplicando la fórmula 40 / N = 40 / 76
Como no disponemos de un disco de 76 agujeros, se debe reducir la fracción mediante simplificación, hasta obtener un denominador correspondiente a uno de los agujeros disponibles (recordar # de agujeros del plato divisor).
40 / 76 = 10 / 19 , mediante simplificación (4ta en numerador y denominador).
Lo cual equivale a 10 agujeros en 19.
Caso B: Cuando N<40 (Ejemplo que muestra el video dispuesto al inicio del tema).
Tomemos como ejemplo N=35, aplicando la fórmula 40 / N = 40 /35 = 1 + 5/35
La manivela efectuará 1 giro + 5/35 de vuelta.
Como no hay disco con 35 agujeros, debemos reducir la fracción así:
5/35 = 1/7 , mediante simplificación (quinta).
1/7 = 3/21 , mediante amplificación (por tres).
Esto corresponde a 1 giro de la manivela+ 3 agujeros en circunferencia 21.
